intersecção entre retas

Equação de uma reta r, conhecidos o coeficiente angular e um ponto de r

   

Seja r uma reta de coeficiente angular m. Sendo P(X₀, Y₀), P  r, e Q(x,y) um ponto qualquer de r(QP), podemos escrever:

Como exemplo, vamos determinar a equação geral da reta r que passa por P(1, 2), sendo m=3. Assim, temos X₀=1  e Y₀=2. Logo:

y-y₀=m(x-x₀)=y-2 = 3(x - 1) = y-2 = 3x - 3 = 3x - y - 1 = 0

que é a equação geral de r.

• Representação gráfica de retas  

 Para representar graficamente as retas de equação ax + by + c = 0 ( b0), isolamos a variável y e atribuímos valores a x, obtendo pares ordenados que são pontos da reta.

   Assim, é mais conveniente usar a equação na forma reduzida, já que ela apresenta o y isolado.

• Coordenadas do ponto de intersecção de retas

  

 A intersecção das retas r e s, quando existir, é o ponto P(x, y), comum a elas, que é a solução do sistema formado pelas equações das duas retas.

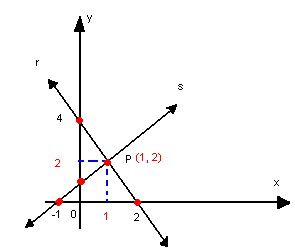
   Vamos determinar o ponto de intersecção, por exemplo, das retas r: 2x +y - 4 =0 e s: x -y +1=0. Montando o sistema e resolvendo-o, temos:

   

Substituindo esse valor em x -y = -1, temos:

1 - y = -1

y = 2

   

Logo, P(1, 2) é o ponto de intersecção das retas r e s.

Graficamente, temos:

Posições relativas entre retas

• Paralelismo

   

Duas retas, r e s, distintas e não-verticais, são paralelas se, e somente se, tiverem coeficientes angulares iguais.

• Concorrência

  

 Dadas as retas r: a₁x +b₁y + c₁ = 0 e s: a₂x + b₂y + c₂ = 0, elas serão concorrentes se tiverem coeficientes angulares diferentes:

        

Como exemplo, vamos ver se as retas r: 3x - 2y + 1 = 0  e  s: 6x + 4y + 3 = 0 são concorrentes:  

• Perpendicularismo

        Se r  e s são duas retas não-verticais, então r é perpendicular a s se, e somente se, o produto de seus coeficientes angulares for igual a -1. Lê-se . Acompanhe o desenho:

• Ângulo entre duas retas

   Sendo r e s duas retas não-verticais e não-perpendiculares entre si, pelo teorema do ângulo externo , temos:

   

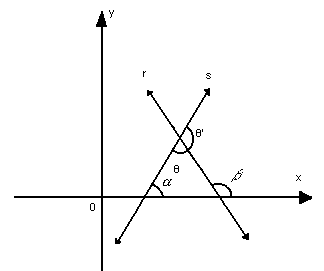
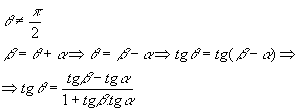
 Dependendo da posição das duas retas no plano, o ângulo  pode ser agudo ou obtuso. Logo:

    

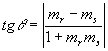
Essa relação nos fornece o ângulo agudo  entre r e s, pois . O ângulo obtuso  será o suplemento de .

• Distância entre ponto e reta

  

 Dados um ponto P(x₁, y₁) e uma reta r:ax + by + c = 0, a distância entre eles (d_pr)é dada por:

Vamos calcular a distância, por exemplo, do ponto P(-1,2) à reta r: x - 2y + 1 = 0.

Temos P(-1, 2) = P(x1, y1), a = 1, b= - 2  e  c=1. Assim:

Exercícios:

Equação Reduzida da Reta

2) Escreva as equações reduzidas das retas determinadas por:

  a) A(2,3) B(0,1)

  b) M(-3,-1) N(2,-5)

 a)

  3x - 0y + 2 - 0 - 2y - x = 0  2x - 2y + 2 = 0    -2y = -2x - 2    y = x + 1

b)

  -x + 2y + 15 + 2 + 3y + 5x = 0   4x + 5y + 17 = 0   5y = -4x - 17    y = -4 x - 17

                                                                                                                                    5       5   

Coeficiente angular

3) Calcule o coeficiente angular das retas de equações:

  a) 3x + 4y - 7 = 0

  b) -6x + 8y + 3 = 0

a) 4y = -3x + 7

      y = -3 x + 7   coeficiente angular = -3

             4       4                                   4

b) 8y = 6x - 3

       y = 6 x - 3 = 3 x - 3     coeficiente angular  = 3

             8      8    4      8                                    4

Intersecção de Retas

4) Determine o ponto de intersecção dos seguintes pares de retas concorrentes:

  a) 3x + 2y - 8 = 0 e 4x + 5y - 13 = 0

  b) 2x - 5y - 2 = 0 e 3x + 5y -28 = 0

a)  3x + 2y = 8   . (-4)     -12x - 8y = -32       7y = 7

     4x + 5y = 13 . (3)       12x + 15y = 39      y = 7 = 1

                                       0x + 7y = 7               7      

3x + 2.1 = 8

  x = 6 = 2          I (2,1)

        3   

b) 2x - 5y = 2       5x = 30            2.6 - 5y = 2

    3x + 5y = 28      x = 30 = 6       -5y = 2 - 12

    5x + 0y = 30            5                y = -10 = 2            I (6,2)

                                                           -5   

Paralelismo m1 = m2

5) Verifique se as retas r e s abaixo são paralelas em cada um dos seguintes casos:

  a) r: 6x + 7y + 3 = 0 e s: 12x + 14y - 21 = 0

  b) r: 5x + 3y - 10 = 0 e s: 5x - 10y - 10 = 0

a) 7y = -6x - 3       14y = -12x - 21 y = -12 x - 21  y = -6 x - 3     

      y = -6 x -3                                    14      14         7     2

             7    7 

coeficiente angular igual, portanto r//s.  m1 = m2

b) 3y = -5x +10      -10y = -5x + 10  y = 5 x - 10  y = 1 x - 1

      y = -5 x + 10                                 10    10        2

             3        3

coeficiente angular diferente, portanto r não paralela a s. m1 diferente de m2

Perpendicularismo m1.m2 = -1

6) Verifique se as retas r e s abaixo são perpendiculares em cada um dos casos:

  a) r: x + 7y - 10 = 0 e s: y = 7x + 3

  b) r: x - y + 7 = 0 e s: 2x + 5y - 7 = 0   

a) r: 7y = -x + 10           s: y = 7x + 3

      y = -1 x + 10                  m1.m2 = -1    -1 . 7 = -7 = -1    r e s são perpendiculares 

             7       7                                         7         7 

b)r:  -y = -x - 7        y = 1x + 7     s: 5y = -2x + 7 

     y = 1 x + 7                                 y = -2 x + 7       1 . -2 = -2   r e s não são perpendiculares e nem paralelas

           1      1                                        5       5             5     5     

http://somatematica.com.br/emedio/retas/retas9.php

                                              videos: