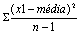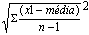Moda e Mediana
A estatística descritiva é a parte da estatística responsável por realizar essa análise, apontando tendências de comportamento das variáveis, criando gráficos e descrevendo as características dos conjuntos pesquisados. Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana.
Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano. Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14} A moda desse conjunto de dados será a idade que mais aparece, ou seja: Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos. Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto, Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia. {35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42} Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser: Mo = 35 ou Mo = 36 Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio. Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente. 1. Mediana de um conjunto de dados com número de elementos ímpar.
exemplo 1
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais. Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol: Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980} Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos. Mediana de um conjunto de dados com número de elementos ímpar.
exemplo 2
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa. Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420 Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980} Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos.
A média aritmética é considerada uma medida de tendência central e é muito utilizada no cotidiano. Surge do resultado da divisão do somatório dos números dados pela quantidade de números somados.
Por exemplo, determinar a média dos números 3, 12, 23, 15, 2.
Ma = (3+12+23+15+2) / 5
Ma = 55 / 5
Ma = 11
A média dos números é igual a 11.
Esse tipo de cálculo é muito utilizado em campeonatos de futebol no intuito de determinar a média de gols da rodada, nas escolas calculando a média final dos alunos, também é utilizado nas pesquisas estatísticas, pois a média dos resultados determina o direcionamento das ideias expressas pelas pessoas pesquisadas.
Calcule a média anual de Carlos na disciplina de Matemática com base nas seguintes notas bimestrais: 1ºB = 6,0 2ºB = 9,0 3ºB = 7,0 4ºB = 5,0
Ma = (6,0 + 9,0 + 7,0 + 5,0) / 4 Ma = 27/4 Ma = 6,75 A média anual de Carlos foi 6,75.
O dólar é considerado uma moeda de troca internacional, por isso o seu valor diário possui variações. Acompanhando a variação de preços do dólar em reais durante uma semana verificou-se as variações de acordo com a tabela informativa:
Segunda
|
Terça
|
Quarta
|
Quinta
|
Sexta
|
R$ 2,30
|
R$ 2,10
|
R$ 2,60
|
R$ 2,20
|
R$ 2,00
|
Determine o valor médio do preço do dólar nesta semana.
Ma = (2,3 + 2,1 + 2,6 + 2,2 + 2) / 5
Ma = 11,2 / 5
Ma = 2,24
O valor médio do dólar na semana apresentada foi de R$ 2,24.
- Média aritmética ponderada
Definição
A média aritmética ponderada é a média dos elementos do conjunto numérico A em relação à adição, onde todos os elementos têm o seu determinado peso.
Calculo da média aritmética ponderada
Sendo x a média aritmética ponderada dos elementos do conjunto numérico A = {x1, x2, x3; …; xn}, com seus respectivos pesos p1; p2; p3; …; pn, nesse caso, temos, por definição:
Note que quando p1 = p2 = p3 = … = pn = 1, nesse caso, temos:
como a média aritmética simples.
Conclusão
Para se obter a média aritmética ponderada dos n elementos do conjunto numérico A, é necessário determinar a soma dos produtos de cada elemento multiplicado pelo respectivo peso, e dividi-la pela soma dos pesos.
Exemplo 1
Na escola de Gabriel, a média anual de cada matéria é calculada de acordo com os princípios da média ponderada. Considerando que o peso das notas esteja relacionado ao bimestre em questão, determine a média anual de Gabriel sabendo que as notas em Matemática foram iguais a:
1º Bimestre: 7,0
2º Bimestre: 6,0
3º Bimestre: 8,0
4º Bimestre: 7,5
A média anual de Gabriel é correspondente a 7,3.
Exemplo 2
Buscando melhorar o atendimento ao usuário do sistema de saúde de um município, a prefeitura realizou uma pesquisa de rendimento satisfatório com 500 pessoas. As notas disponibilizadas aos entrevistados no intuito de avaliar o nível de satisfação compreendem a notas inteiras de 1 a 10. Veja os resultados na tabela a seguir:
A média de satisfação dos usuários do sistema de saúde do município em questão foi igual a 5,0.
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola






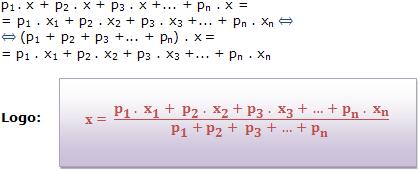
.jpg)
.jpg)
.jpg)