medidas de dispersao

• MEDIDAS DE DISPERSÃO

Um aspecto importante no estudo descritivo de um conjunto de dados, é o da determinação da variabilidade ou dispersão desses dados, relativamente à medida de localização do centro da amostra.
Supondo ser a média, a medida de localização mais importante, será relativamente a ela que se define a principal medida de dispersão - a variância, apresentada a seguir.

• Variância 

Define-se a variância, como sendo a medida que se obtém somando os quadrados dos desvios das observações da amostra, relativamente à sua média, e dividindo pelo número de observações da amostra menos um.
   

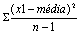
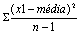
• Desvio-padrão 

Uma vez que a variância envolve a soma de quadrados, a unidade em que se exprime não é a mesma que a dos dados. Assim, para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados, tomamos a raiz quadrada da variância e obtemos o desvio padrão:
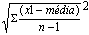
O desvio padrão é uma medida que só pode assumir valores não negativos e quanto maior for, maior será a dispersão dos dados.
Algumas propriedades do desvio padrão, que resultam imediatamente da definição, são:
o desvio padrão será maior, quanta mais variabilidade houver entre os dados.
   

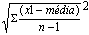
Exemplo

Observe as notas de três competidores em uma prova de manobras radicais com skates.

Competidor A: 7,0 – 5,0 – 3,0

Competidor B: 5,0 – 4,0 – 6,0

Competidor C: 4,0 – 4,0 – 7,0 
Ao calcular a média das notas dos três competidores iremos obter média cinco para todos, impossibilitando a nossa análise sobre a regularidade dos competidores.
Partindo dessa ideia, precisamos adotar uma medida que apresente a variação dessas notas no intuito de não comprometer a análise.

Variância e Desvio Padrão

A variância é calculada subtraindo o valor observado do valor médio. Essa diferença é quanto um valor observado se distância do valor médio. Observe os cálculos:

Competidor A



Competidor B



Competidor C




Desvio Padrão

É calculado extraindo a raiz quadrada da variância.

Competidor A
√2,667 = 1,633

Competidor B
√ 0,667 = 0,817

Competidor C
√2 = 1,414

Podemos notar que o competidor B possui uma melhor regularidade nas notas.

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Exercício 1 

Conhecem-se as seguintes idades (em anos) de todos os 6 gorilas do zoo da cidade:

9,1,16,11,10,14

Qual é a média de idades dos gorilas do zoo? Qual é a variância?

Resolução

Porque temos os dados das idades de todos os 6 gorilas do zoo, somos capazes de calcular a
média da população (μ)e a variância da população (σ2).

Para encontrar a média da população, somam-se todas as 6 idades e divide-se por 6.

μ=∑i=1NxiN=∑i=16xi6

μ=9+1+16+11+10+146=10.2 anos de idade

Encontrar os quadrados dos desvios de cada gorila

Idade xi	Desvio (xi−μ)	(xi−μ)2
9 anos	−1.2 anos	1.44 anos2
1 ano	−9.2 anos	84.64 anos2
16 anos	5.8 anos	33.64 anos2
11 anos	0.8 anos	0.64 anos2
10 anos	−0.2 anos	0.04 anos2
14 anos	3.8 anos	14.44 anos2

Porque usamos a média da população (μ)para calcular os quadrados do desvios, podemos encontrar avariância (σ2), sem introduzir qualquer enviesamento, simplesmente calculado a média dos quadrados dos desvios:

σ2=∑i=1N(xi−μ)2N

σ2=1.44+84.64+33.64+0.64+0.04+14.446

σ2=134.846=22.47 anos2

Cada gorila tem em média 10.2 anos, e a variância da população é de 22.47 anos2.