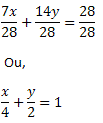Geometria Analitica

Área de Triângulo

Na geometria plana encontramos a área de um triângulo fazendo uma relação com o valor de suas dimensões, e na trigonometria, com o valor do seno de um ângulo interno relacionado com os lados do triângulo é possível também encontrar a sua área.

A geometria analítica também possui seus artifícios para o cálculo da área de um triângulo, nesse caso é necessário que saibamos as coordenadas de seus três vértices para que o triângulo possa ser representado em um plano cartesiano.

Considere o triângulo de vértices A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C), veja a sua representação em um plano cartesiano:

 

A partir dessa representação podemos dizer que o cálculo da área (A) de um triângulo através dos conhecimentos da geometria analítica é dado pelo determinante dos vértices dividido por dois. 

A = |D|
        2
 

 Onde D =

Exemplos: A área de um triângulo é 25/2 e seus vértices são (0,1), (2,4) e (-7,k). Nesse caso qual será o possível valor de k?

Sabemos que a área A = |D|, portanto é preciso que encontremos o valor de D.
                                        2 

D =

D = -7 + 2k + 28 -2
D = 2k + 19

Substituindo a fórmula teremos:

A = |D|
       2

25= 2k + 19
 2           2

25 = 2k + 19
25 – 19 = 2k
6 = 2k
6:3 = k
k = 3


http://www.mundoeducacao.com/matematica/area-um-triangulo-pela-geometria-analitica.htm


exercícios:

1) Determinar a área do triângulo a seguir considerando que a sua base mede 23 metros e a altura 12 metros.

2) Calcule a área do triângulo a seguir: 

p = (9 + 7 + 14) / 2
p = 30 / 2
p = 15

A = √15(15 – 9)(15 – 7)(15 – 14)
A = √15 * 6 * 8 * 1
A = √720
A = 26,83 cm2(aproximadamente)

3) Um triângulo possui lados medindo 5 cm e 8 cm, respectivamente. Sabendo que ele possui um ângulo na base medindo 30º, determine a área desse triângulo.

vídeo:

Distância de um ponto a uma reta

A distância entre um ponto e uma reta é calculada unindo o próprio ponto à reta através de um segmento, que deverá formar com a reta um ângulo reto (90º). Para estabelecer a distância entre os dois necessitamos da equação geral da reta e da coordenada do ponto. A figura a seguir estabelece a condição gráfica da distância entre o ponto P e a reta r, sendo o segmento PQ a distância entre eles.

Existem várias distâncias entre o ponto P e a reta s, assim como existem vários caminhos até um destino. Mas para nós interessa somente a menor distância.

A distância entre P e t é dada pela fórmula:

Onde, a, b e c são os coeficientes da equação da reta s e x_o e y_o são as coordenadas do ponto P.

Exemplo 1.

Calcule a distância entre o ponto P(0, 10) e a reta s: x – y + 1 = 0.

Solução: Da equação geral da reta s, obtemos: a = 1, b = – 1 e c = 1.

Segue que:

 

Exemplo 2.

Determine a que distância está o ponto A(– 2, 3) da reta t: 4x + 3y – 2 = 0.

Solução: Da equação da reta t, obtemos: a = 4, b = 3 e c = – 2.

Segue que:

http://www.alunosonline.com.br/matematica/distancia-entre-ponto-reta.html


exercícios:

Questão 01.Dado o ponto B com coordenadas (2, 6) e reta s: 2x + 4y – 1 = 0, determine a distância entre eles de acordo com os conceitos e fundamentos da Geometria Analítica.  

Resposta 

Questão 2

(Fuvest-SP)
Calcule a distância entre a reta r1, de equação 3y = 4x – 2, e a reta r2, de equação 3y = 4x + 8, sabendo que r1//r2.

Resposta 

vídeo:

Ângulos entre retas

Considere duas retas distintas e concorrentes do plano, r e s, ambas oblíquas aos eixos coordenados e não perpendiculares entre si. As duas retas formam um ângulo entre si, que denominaremos de α. Esse ângulo α é tal que:

Onde m_s e m_r são os coeficientes angulares das retas s e r, respectivamente.
Se ocorrer de uma das retas ser vertical e a outra oblíqua, o ângulo α formado entre elas é tal que:

Exemplo 1. 

Determine o ângulo formado entre as retas r: x - y = 0 e s: 3x + 4y – 12 =0

Solução: Para determinar o ângulo formado entre as duas retas, precisamos conhecer o coeficiente angular de cada uma delas. Assim, vamos determinar o coeficiente angular das retas r e s.

Para a reta r, temos:

x - y = 0
y = x

Portanto, m_r = 1.
Para a reta s, temos:

 Portanto, m_s = -3/4

Conhecendo os valores dos coeficientes angulares, basta aplicar a fórmula do ângulo entre duas retas:

Exemplo 2.

 Determine o ângulo formado entre as retas r: y = 3x + 4 e s: y = – 2x + 8.

Solução: Vamos determinar o coeficiente angular de cada uma das retas dadas.

Para a reta r, temos:
y = 3x + 4
m_r = 3
Para a reta s, temos:
y = – 2x + 8
m_s = – 2

Aplicando a fórmula do ângulo entre duas retas, obtemos: 

http://www.mundoeducacao.com/matematica/angulo-formado-entre-duas-retas.htm



Exercícios:

Questão 01.Determine os valores de x e y nas figuras a seguir:

Resposta 

Os ângulos 15x – 45 e 12x – 15 são opostos pelo vértice, portanto são iguais.
15x – 45 = 12x – 15
15x – 12x = 45 – 15
3x = 30
x = 10º
Os ângulos 15x – 45º e y são suplementares, isto é, a soma entre eles resulta em 180º.
15x – 45 + y = 180
15 * 10 – 45 + y = 180
150 – 45 + y = 180
105 + y = 180
y = 180 – 105
y = 75º

 Questão 02.Calcule o valor de x na figura.

Resposta 

Os ângulos da figura são complementares, isto é, a soma entre eles é igual a 90º.
x + 40 + 3x + x – 10 = 90
5x + 30 = 90
5x = 90 – 30
5x = 60
x = 12

Questão 03.(FAM–SP) Dadas às retas r e s, paralelas entre si, e t, concorrente com r e s, calcule o valor de x:

a) 51º

b) 35º

c) 90º

d) 50º

e) 45º

Resposta 

Os ângulos são suplementares, isto é, a soma entre eles é igual a 180º.
2x + 30 + x = 180
3x = 180 – 30
3x = 150
x = 150/3
x = 50º
Resposta correta alternativa d.



vídeo:

Posição relativa entre duas retas no plano.

• Paralelas

Considere duas retas distintas e paralelas r e s:

Temos que:

r ∕∕ s ↔ tg α₁ = tg α₂ ou m_r = m_s

Isso quer dizer que duas retas são paralelas se, e somente se, seus coeficientes angulares forem iguais.


Exemplo 1.

Verifique se as retas r: y = 3x – 2 e s: 6x – 2y + 5 = 0 são paralelas.

Solução: Precisamos determinar o coeficiente angular das retas r e s.

Vamos determinar o coeficiente angular da reta r:

Como a equação da reta r está na forma reduzida, fica fácil ver que mr = 3.

Agora vamos determinar o coeficiente angular da reta s.
6x – 2y + 5 = 0
2y = 6x + 5
y = 3x + 5/2

Daí, vemos que m_s = 3

Como m_r =m_s =3, podemos afirmar que r // s.


Exemplo 2.

Para quais valores de k as retas 3x + 2y – 1 = 0 e kx – 3y + 1 = 0 são paralelas?

Solução: Para as duas retas serem paralelas, os seus coeficientes angulares devem ser iguais. Assim, vamos determinar o coeficiente angular das retas em questão.


s:3x+2y-1=0

2y= -3x+1

y= -3x/2 + 1/2

ms= -3/2


r: kx-3y+1 =0

-3x= -kx - 1

y= kx/3 + 1/3

mr = 1/3

Daí segue que:

ms=mr

-3/2 = k/3

k = -9/2

• Concorrentes

Duas retas são concorrentes se, somente se, possuírem um ponto em comum, ou seja, a intersecção das duas retas é o ponto em comum.

Considerando a reta t e u e as suas respectivas equações gerais das retas, a_tx + b_ty + c_t = 0 e a_ux + b_uy + c_u = 0. Representando-as em um plano cartesiano, iremos perceber que são concorrentes, pois possui o ponto A em comum.

Exemplo: As equações gerais das duas retas r e s são respectivamente, x + 4y – 7 = 0 e 3x + y + 1 = 0. 


Determine o ponto P(x0, y0) comum às retas r e s.

Sabemos que o ponto de intersecção de duas retas concorrentes é a solução do sistema formado por elas. Assim, veja a resolução do sistema abaixo:

x + 4y – 7 = 0
3x + y + 1 = 0

x + 4y = 7     (-3)
3x + y = -1

-3x  –  12y   = -21
 3x   +   y      = -1
           -11y   = -22
y = 2

Substituindo o valor de y em qualquer uma das equações iremos obter o valor de x:

x + 4y = 7
x + 4 . 2 = 7
x + 8 = 7
x = 7 – 8
x = -1

Portanto, o ponto P(x₀, y₀) = (-1,2).

No início da explicação foi dito que as retas t: a_tx + b_ty + c_t = 0 e u: a_ux + b_uy + c_u = 0 são concorrentes. Para que seja verdadeira essa afirmação o sistema formado por elas deverá ser possível e determinado, essa verificação irá funcionar da seguinte forma:

a_tx + b_ty + c_t = 0
a_ux + b_uy + c_u = 0

a_tx + b_ty = - c_t
a_ux + b_uy = - c_u

E para que esse sistema seja possível e determinado, o seu determinante deverá ser diferente de zero.

 

Exemplo: Verifique se as retas 2x + y – 3 = 0 e 6x + 5y + 1 = 0 são concorrentes.

2x + y = 3
6x + 5y = -1

2 . 5 – (1 . 6) ≠ 0
10 – 6 ≠ 0
4 ≠ 0

• Coincidentes

Duas retas são coincidentes se pertencem ao mesmo plano e possuem todos os pontos em comum.

• Perpendiculares

Sabemos da Geometria Plana que duas retas são perpendiculares quando são concorrentes e formam entre si um ângulo reto (90º) . Sejam as retas r: y = m_r x + n_r e s: y = m_s x + n_s . Nestas condições podemos escrever a seguinte relação entre os seus coeficientes angulares:
m_s = - 1 / m_r ou m_r . m_s = -1 .
Dizemos então que se duas retas são perpendiculares, o produto dos seus coeficientes angulares
é igual a -1.

Exemplo:

Dadas as retas de equações (2w - 2)x + (w - 1)y + w = 0 e (w - 3)y + x - 2w = 0, podemos afirmar que:

a) elas são perpendiculares para qualquer valor de w
b) elas são perpendiculares se w = 1
c) elas são perpendiculares se w = -1
d) elas são perpendiculares se w = 0
e) essas retas não podem ser perpendiculares

Solução:
Podemos escrever para a 1ª reta: y = [-(2w-2) / (w-1)].x - w /(w-1).
Analogamente para a 2ª reta: y = [-1 / (w-3)].x + 2w / (w-3). Ora, os coeficientes de x são os coeficientes angulares e, pelo que já sabemos, a condição de perpendicularidade é que o produto desses coeficientes angulares seja igual a -1. Logo:

Efetuando os cálculos indicados e simplificando-se obtemos: w² - 2w + 1 = 0, que é equivalente a
(w - 1)² = 0, de onde conclui-se que w = 1.

Mas, cuidado! Observe que 1 anula o denominador da expressão acima e, portanto é uma raiz estranha, já que não existe divisão por zero! Apesar das aparências, a raiz 1 não serve! Logo, a alternativa correta é a letra E e não a letra B como ficou aparente.

http://www.alunosonline.com.br/matematica/paralelismo.html 
http://www.mundoeducacao.com/matematica/interseccao-retas-concorrentes.htm 
http://deborampmatematica.blogspot.com.br/2011/08/retas-paralelas-retas-concorrentes.html


Exercícios:

Verifique o posicionamento da reta r, dada pela equação 2x + y – 1 = 0 em relação à circunferência de equação x² + y² + 6x – 8y = 0. 

Resposta 

  Questão 01.Determinar as coordenadas do centro da circunferência é a medida do raio:

x² + y² + 6x – 8y = 0
x² + 6x + y² – 8y = 0
x² + 6x →  completando o trinômio
x² + 6x + 9 = (x + 3)²
y² – 8y → completando o trinômio
y² – 8y + 16 = (y – 4)²
x² + 6x + y² – 8y = 0
x² + 6x + 9 + y² – 8y + 16 = 9 + 16
(x + 3)² + (y – 4)² = 25

A fórmula geral de uma equação da circunferência é dada por (x – a)² + (y – b)² = r², dessa forma:
Coordenadas do centro: (–3; 4)
Medida do raio: 5
Determinando a distância entre o centro e a reta
Reta r: 2x + y – 1 = 0



Temos que a distância é menor que o raio, pois 1,3 < 5. Dessa forma, a reta é secante à circunferência.

  Questão 02.Dada a reta s representada pela equação 2x – y + 1 = 0 e a circunferência de equação
x² + y² – 2x = 0, determine a posição relativa entre elas.  

Resposta 

Vamos estabelecer um sistema entre as duas equações:

Reta: 2x – y + 1 = 0
Circunferência: x² + y² – 2x = 0

Resolvendo o sistema pelo método da substituição:

Isolando y na 1ª equação:

2x – y + 1 = 0
– y = –1 – 2x
y = 1 + 2x

Substituindo y na 2ª equação:

x² + (1 + 2x)² – 2x = 0

x² + 1 + 4x + 4x² – 2x = 0
5x² + 2x + 1 = 0

∆ = b² – 4ac
∆ = 2² – 4 * 5 * 1
∆ = 4 – 20
∆ = –16

Quando ∆ < 0, a equação não possui raízes. Dessa forma o sistema não possuirá soluções. Portanto, a reta é externa à circunferência.

Questao 03.Determine o valor de w sabendo que a reta de equação x – y + w = 0 é tangente à circunferência de equação x² + y² = 9. 

Resposta 

Se a reta é tangente à circunferência, temos que a distância do centro até a reta possui a mesma medida do raio.

Em razão da equação x² + y² = 9, podemos dizer que o centro corresponde a (0; 0) e o raio igual a 3, pois x² + y² = 9 → (x + 0)² + (y + 0)² = 3².

Distância do centro (0; 0) à reta x – y + w = 0, onde a = 1, b = –1 e c = w:

Calculando w de acordo com d = r:

O valor de w é igual a + 3√2 ou –3√2.

 Questão 04.Determine o comprimento da corda determinada pela intersecção da reta r, de equação x + y – 1 = 0, com a circunferência de equação x² + y² + 2x + 2y – 3 = 0. 

Resposta

AB = medida da corda
CM = distância entre centro e reta
AM = metade da medida da corda → AB/2.

No triângulo AMC aplicaremos o teorema de Pitágoras, mas para isso precisaremos determinar a distância CM e o raio da circunferência, dado por CA.

Centro da circunferência

x² + y² + 2x + 2y – 3 = 0
x² + 2x + y² + 2y = 3
x² + 2x + 1 + y² + 2y + 1 = 3 + 1 + 1
(x + 1)² + (y + 1)² = 5

Centro (–1, –1) e raio = √5.
Reta: x + y – 1 = 0


A medida da corda AB de acordo com a situação proposta é AB = √2.

vídeo:

Coeficiente Ângular

Sabemos que o valor do coeficiente angular de uma reta é a tangente do seu ângulo de inclinação. Através dessa informação podemos encontrar uma forma prática para obter o valor do coeficiente angular de uma reta sem precisar fazer uso do cálculo da tangente.

Vale ressaltar que se a reta for perpendicular ao eixo das abscissas, o coeficiente angular não existirá, pois não é possível determinar a tangente do ângulo de 90º.

Para representarmos uma reta não vertical em um plano cartesiano é preciso ter no mínimo dois pontos pertencentes a ela. Desse modo, considere uma reta s que passa pelos pontos A(xA, yA) e B(xB, yB) e possui um ângulo de inclinação com o eixo Ox igual a α.

Prolongado a semirreta que passa pelo ponto A e é paralela ao eixo Ox formaremos um triângulo retângulo no ponto C.

O ângulo A do triângulo BCA será igual ao da inclinação da reta, pois, pelo Teorema de Tales, duas retas paralelas cortadas por uma transversal formam ângulos correspondentes iguais.

Levando em consideração o triângulo BCA e que o coeficiente angular é igual à tangente do ângulo de inclinação, teremos:

tgα = cateto oposto / cateto adjacente

tgα = y_B – y_A / x_B – x_A

Portanto, o cálculo do coeficiente angular de uma reta pode ser feito pela razão da diferença entre dois pontos pertencentes a ela.

m = tgα = Δy / Δx  


Exemplo 1

Qual é o coeficiente angular da reta que passa pelos pontos A (–1,3) e B (–2,4)?

m = Δy/Δx

m = 4 - 3 / (-2) - (-1)
m = 1 / -1
m = -1 


Exemplo 2

O coeficiente angular da reta que passa pelos pontos A (8,1) e B (9,6) é:

m = Δy/Δx

m = 6 – 1/9 – 8
m = 5/1
m = 5 

http://www.brasilescola.com/matematica/calculo-coeficiente-angular-uma-reta.htm


exercicios:

1. Qual é o coeficiente angular da reta que passa pelos pontos A (–1,3) e B (–2,4)?

2. O coeficiente angular da reta que passa pelos pontos A (8,1) e B (9,6) é?

3. Determine K, sabendo que a inclinação da reta que passa pelos pontos A(K, 3) e B(-1 , -4) é de 45°.

4. O coeficiente angular de uma reta é m = - 2/3. Ache a equação dessa reta sabendo que ela passa pelo ponto (4, - 2).

5. Determine a equação da reta que passa pelo ponto P(2, 5) e tem uma inclinação de 60°.

Gabarito:
1) m = -1;
2) m = 5;
3) K = 6;
4) 2x + 3y - 2 = 0;
5) V3x - y + 5 - 2V3 = 0 (legenda V = raiz quadrada).

http://eduardomachado9050.blogspot.com.br/2013/05/coeficiente-angular-exercicios.html


video:

Estudo das Retas

Equação Geral 

Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.

Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:

Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos A ≠ B,temos:  

ax+by+c=0 (equação geral da reta r)

Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):

se am + bn + c = 0, P é o ponto da reta;
se am + bn + c ≠ 0, P não é ponto da reta.

• Exemplo:

 Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:

Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior.
Substituindo as coordenadas de P em x - y + 2 = 0, temos:
 -3 - (-1) + 2 = 0 -3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P pertence a r
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
 1 - 2 + 2 ≠ 0

 Como a igualdade não é verdadeira, então Q pertence a r


   Equação Reduzida da Reta 

  Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):

y-q=m(x-0)
 y-q=mx
 y=mx+q

Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:

Onde:

Exemplo 1: 

 Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:

 y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8 y = 4x – 8 + 7
y = 4x – 1  


Equação Segmentada da Reta

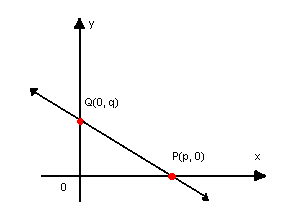
  Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q), com p ≠ 0 e q ≠ 0

A equação geral de r é dada por:

Dividindo essa equação por pq (pq ≠ 0) temos:

Exemplo:

 Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.

 Solução:
  
Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:

 7x + 14y = 28 Dividindo toda igualdade por 28, obtemos:

Que é a equação segmentária da reta t.

Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:

(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.

Questões:

01. (FEI) As retas 2x - y = 3 e 2x + ay = 5 são perpendiculares. Então:

a) a = -1
b) a = 1
c) a = -4
d) a = 4
e) n.d.a.

 02.(USP) A equação da reta que passa pelo ponto (3; 4) e é paralela à bissetriz do 2° quadrante é:
 
a) y = z - 1
b) x + y - 7 = 0
c) y = x + 7
d) 3x + 6y = 3
e) n.d.a.

 03.As retas 3x + 2y - 1 = 0 e -4x + 6y - 10 = 0 são:
 
a) paralelas
b) coincidentes
c) perpendiculares
d) concorrentes e não perpendiculares
e) n.d.a.
 

 04.(USP) A equação da reta passando pela origem e paralela à reta determinada pelos pontos A(2; 3) e B(1; -4) é:
 
a) y = x
b) y = 3x - 4
c) x = 7y
d) y = 7x
e) n.d.a

 01. D

  02. B

  03. C

  04. D

 http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/estudo-da-reta

Video: