Equação Geral
Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.
Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico, também de r, estando A, B e P alinhados, podemos escrever:
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos A ≠ B,temos:
ax+by+c=0 (equação geral da reta r)
Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):
se am + bn + c = 0, P é o ponto da reta;
se am + bn + c ≠ 0, P não é ponto da reta.
- Exemplo:
Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:
Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior.
Substituindo as coordenadas de P em x - y + 2 = 0, temos:
-3 - (-1) + 2 = 0 -3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P pertence a r
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
1 - 2 + 2 ≠ 0
Como a igualdade não é verdadeira, então Q pertence a r
Equação Reduzida da Reta
Vamos determinar a equação da reta r que passa por Q(0,q), e tem coeficiente angular m = tg(α):
y-q=m(x-0)
y-q=mx
y=mx+q
Toda equação na forma y = mx + q é chamada equação reduzida da reta, em que m é o coeficiente angular e q a ordenada do ponto n qual a reta cruza o eixo Oy. A equação reduzida pode ser obtida diretamente da equação geral ax + by + c = 0:
Onde:
Exemplo 1:
Utilizando o ponto P1(2, 7), no qual x = 2 e y = 7, temos:
y – y1 = a * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8 y = 4x – 8 + 7
y = 4x – 1
Equação Segmentada da Reta
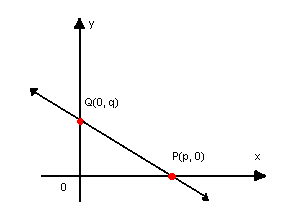
Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q), com p ≠ 0 e q ≠ 0
A equação geral de r é dada por:
Dividindo essa equação por pq (pq ≠ 0) temos:
Exemplo:
Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.
Solução:
Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:
7x + 14y = 28 Dividindo toda igualdade por 28, obtemos:
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
Questões:
01. (FEI) As retas 2x - y = 3 e 2x + ay = 5 são perpendiculares. Então:
a) a = -1
b) a = 1
c) a = -4
d) a = 4
e) n.d.a.
a) a = -1
b) a = 1
c) a = -4
d) a = 4
e) n.d.a.
02.(USP) A equação da reta que passa pelo ponto (3; 4) e é paralela à bissetriz do 2° quadrante é:
a) y = z - 1
b) x + y - 7 = 0
c) y = x + 7
d) 3x + 6y = 3
e) n.d.a.
a) y = z - 1
b) x + y - 7 = 0
c) y = x + 7
d) 3x + 6y = 3
e) n.d.a.
03.As retas 3x + 2y - 1 = 0 e -4x + 6y - 10 = 0 são:
a) paralelas
b) coincidentes
c) perpendiculares
d) concorrentes e não perpendiculares
e) n.d.a.
a) paralelas
b) coincidentes
c) perpendiculares
d) concorrentes e não perpendiculares
e) n.d.a.
04.(USP) A equação da reta passando pela origem e paralela à reta determinada pelos pontos A(2; 3) e B(1; -4) é:
a) y = x
b) y = 3x - 4
c) x = 7y
d) y = 7x
e) n.d.a
a) y = x
b) y = 3x - 4
c) x = 7y
d) y = 7x
e) n.d.a
01. D
02. B
03. C
04. D
Video:







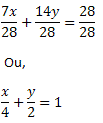


Nenhum comentário:
Postar um comentário